https://www.acmicpc.net/problem/11660
11660번: 구간 합 구하기 5
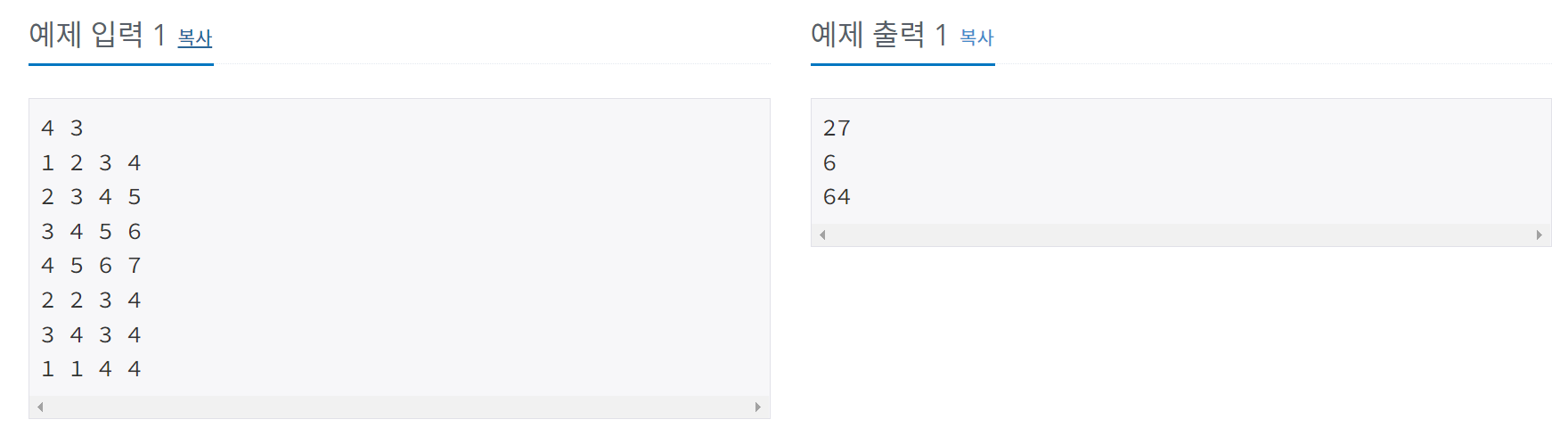
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
🔔 문제 :
(1<= N <= 1024)인 NxN 크기의 표가 있습니다.
(x1,y1) , (x2,y2) 까지 합을 구해야 합니다. (x,y) x행 y열을 의미합니다.
(1<= M <= 100,000) 인 M개의 테스트케이스의 답을 각각 출력해야 합니다.
입력값으론 N, M , 표에 들어가는 숫자들
M개의 줄로 이루어진 x1,y1,x2,y2가 주어집니다.
🔔 Kick Point :
cin, cout을 사용하려면 연결을 끊어줘야지 시간대가 나옵니다. 그래서 무조건
ios::sync_with_stdio(false)
cin.tie(NULL)
cout.tie(NULL) 을 해줘야지 통과가 됩니다.
문제를 풀 땐 저는 표에 있는 수들을 입력받을 때 (1,1) 에서 (x,y) 까지의 숫자 구간 합을 계산해서 넣어주었습니다.
예를 들면
1 1
1 1
이라는 숫자 표가 있으면
1 2
2 3
이라는 구간합 표를 따로 만들어줬습니다.
이후에, arr[y2][x2] - arr[y2][x1 -1] - arr[y1 -1][x2] + arr[y1 -1][x1 -1] 이라는 공식으로 한 번에 구해줍니다.
즉, 아래와 같은 구간합 표가 있고, (2,2) 부터 (2,2) 까지의 구간합을 구하고 싶다면
1 2
2 3
식에 맞게 3 (2,2) - 2(1,2) -2(2,1) + 1(1,1)을 해주면 2,2 의 구간합을 구하게 되어 구간합을 구할때는 O(1) 시간복잡도로 계산할 수 있습니다.
🔔 Code :
#include <iostream>
using namespace std;
int n, m;
int arr[1024][1024];
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
for (int i = 0; i < n; i++) {
int prevCol(0);
for (int j = 0; j < n; j++) {
int tmp2; cin >> tmp2;
prevCol += tmp2;
arr[i][j] = prevCol;
if (i != 0) arr[i][j] += arr[i - 1][j];
}
}
while (m--) {
int y1, x1, y2, x2; cin >> y1 >> x1 >> y2 >> x2;
y1--, x1--, y2--, x2--;
int sum(0);
sum += arr[y2][x2];
if (x1 != 0) { sum -= arr[y2][x1 - 1]; }
if (y1 != 0) { sum -= arr[y1 - 1][x2]; }
if (x1 != 0 && y1 != 0) { sum += arr[y1 - 1][x1 - 1]; }
cout << sum << '\n';
}
}